Differentiation

• Edexcel- C1 Differentiation
• AQA- C1 Differentiation
• OCR- C1 Differentiation

One of the new topics, we learn in A-Level Maths is Differentiation. It is one of the branches of Calculus, which is a major field in Mathematics, and almost is a useful application in loads of other fields.. Engineering, Economics, Physics and Chemistry. It is concerned with how one thing changes, as a result of another quantity changes. E.g. How displacement changes, as time changes (dd/ dt) would be the velocity.... We shall look for now at how y changes with respect to x (we call this dy/dx) = d (delta which means change)

We will look at curves, where the gradient is changing at each point on the curve. So dy/dx on each point is different, and not constant. First, i'll introduce you to a tangent. A tangent, is a straight line which touches a point on the curve, it only touches that point though.

The green line is the tangent to the curve( in black), this tangent only touches the yellow point on the curve. Note the gradient at the yellow point, is different to the rest of the points on the curve, because the gradient changes as x changes.

The derivative of a curve is the same as the dy/dx of a function e.g.

The derivative of x^3 = 3x^2
dy/dx (x^3) = 3x^2
This is the first derivative, if differentiate again, we would get the second derivative, again.. the third.. and so on..

dy / dx means differentiating y with respect to x. (what is happening to y, as x changes)

How to Differentiate

To differentiate a function, you reduce the power by 1, and multiply by the new power :

Function          Derivative
axⁿ                 anx<sup>n-1

e.g. x^2 
dy/dx = 2x


x^3 
dy/dx = 3x^2


* If we had to differentiate anything to the first power e.g. x , 3x, 5x... it would be 1,3 and 5 respectively. Why ? 
Because it is to the power 1, reducing the power to 0.. anything to the power of 0 equals 1 .. so we just multiply the coefficient of x by 1.. which is the same as taking away the x.

*Differentiating a number .. gives 0. Think about it, if draw a graph of say y = 5, the gradient is 0.

Other Notation 

A function can be written as y =... or f(x) = ..., if we have a function defined as f(x) =...., then the derivative of that is f'(x)=...

f(x) = 5x ... f '(x) = 5 (this is called f prime)

*For the first derivative we use one dash.. second derivative two..etc 
We can only differentiate functions in the form of</sup> axⁿ    , so if it looks any different, we have to rearrange to get in that form, using rules of indices.

Sequences and Series

•  Edexcel - C1, Sequences and Series
• AQA - C2, Sequences and Series
• OCR - C2, Sequenes and Series

A sequence is a list of numbers, in it's basic definition. This list can be of a finite / infinite length.e.g. 2,4,6,8.. is a sequence of all positive even numbers. There are many types of sequences, we shall be looking at the Arithmetic Series / Progression.

A series is the sum of the terms in a sequence. Again these can be finite and infinite, depending on the sequence itself.

Arithmetic Sequences

An Arithmetic Sequence is a sequence of numbers, such that difference between the terms is a constant. e.g. 5,9,13,17,21 .. this difference here is + 4. This difference is called the common difference.


Each number in the sequence, is called a term. We call the first term (u1), second term (u2), third term (u3)... and so on. This is just notation. In the previous sequence example, 5 would be the first term, 9 the second, 13 the third.. and so on. The first term of a sequence is a. While the common difference is d.

Nth term, is a rule for finding any term in the sequence. Say if i wanted to find the 28th term of the previous sequence, it would be very long to add 4 each time, to get till the 28th term. Instead we can form a rule to find any term in that sequence. The formula for finding the nth term of a sequence is :

U(n) = a + (n-1)d

a = first term
d= common difference
n = the term you're finding

*This formula will work for any Arithmetic Sequence.

How we got this formula ?
As you know the first term is a. If each term goes up by a common difference, the second term must be a + d. The third term must be a + d + d = a + 2d, The fourth term must be a + d + d + d = a +3d.... and so on... if we look for the nth term it must be a + (n-1)d.


Example
a) Say we have an arithmetic sequence with the first term being 9. The common difference is -4. Find the 80th term ?

Here a is 9, d = -4 , and n=80

Use the formula U(80) = 9 + (80-1)*-4
=9 + (79*-4)
= 9+-(316)
= -307

Arithmetic Series

We also need to be able to find the Sum of an Arithmetic Sequence. There is a formula, we also need to be able to prove that formula (abit confusing, i'll include it in my image notes).

S(n) = The sum of n terms
n = the number of terms
a1 = first term (a)
d = common difference

Example

2,5,8,11,14,17....
a) Find the sum of the first ten terms
b) Find the sum of the terms starting from the 11th term and ending with the 28th term.

Identify a and d.
a = 2, d = +3

a) Use the Formula : 
S(10) =  10/2 [ 2(2) + (10-1)3]
= 5 [4 + 9(3)]
= 5 [4 + 27]
= 5 *31
=155

b) Use the Formula, note a is different.

They want to start from the 11th term, so the 11th term will be a.
 Use the nth term formula to find the 11th term : (Here we use a as 2)

=2 + (11-1)*3
= 2 + (10)*3
= 2 + 30
=32

11th term is 32, which is the a

Count how many terms are from 11 to 28. (18 terms), Now use the formula :
S(18) = 18/2 [ 2(32) + (18-1)*3]
= 9 [64 + 17*3]
= 9 [64 + 51]
= 9 x115
= 1035

Sigma Notation

The sigma sign Σ, is another notation you need to be able to interpret. It is simply the summation of an arithmetic sequence. I will use an example to make you understand it:

Here is an example, for sigma notation. The actual sign Σ means the sum. Now k^2, is the function / rule. The first term we have to add is below the sign, which is 2. So a =2, we have to add all the terms from 2 till 6. The number above the sign, is where we end. So the sum is 2 squared + 3 squared + 4 squared + 5 squared + 6 squared.. = 90.

Proof for the Sum of Arithmetic Series

Equation of a Straight Line

•  Edexcel - C1, Coordinate Geometry
• AQA - C1, Coordinate Geometry
• OCR -C1, Coordinate Geometry

Now we move on to Chapter 2, which involves Straight Lines in the x,y plane. As we know we can write linear equations in the form: y =mx + c, where m is the gradient and c is the y-intercept. We can write linear equations in two other forms one is ax + by + c = 0, where a,b,c are real numbers. Also we can rewrite it in the form y - y1 = m(x -x1), where x1,y1 are the x,y coordinates of a point on the line, and m being the gradient.


The latter form will be used a lot, as we need to be able to find the equation of a straight line, when we are given
a) Two points on the line
b) The Gradient and a point

To rearrange from the form y = mx + c, to ax + by + c = 0, is simple. Let's use an example :
If y = 3x + 5, where m =3 and c=5... Rearrange into the ax + by + c form :
3x - y + 5 =0, Done, we took y to the other side.
a = 3, b = -1 , and c=5.

We use this form because when y = mx + c, contains fractions it can look not so concise. This form is better in that respect.

Given two points

When we are given two point, and we need to find the equation of a line through the points. It is fairly simple.
1) First find the gradient of the line
Remember Gradient = dy/ dx (change in y / change in x)
This should give you the m, in the form y= mx +c.

2) Using one the points, use the equation form [  y - y1 = m(x-x1)  ], where x1, and y1 are the x,y coordinates of the point, and m is the gradient.
3) Substitute in the values, and multiply out the brackets, and simplify either in the form y=mx + c OR ax + by + c=0, usually stated in the question.

Example

Find the equation of a straight line through the points (3,7) and (4,10)

1) Find Gradient = (10 -7) / (4- 3)

= 3 /1

=3

m is 3.

2) Use of the points (3,7) or (4,10) and the gradient (3), substitute into the formula : y-y1 = m(x-x1)

Let's use 3,7

y-7 = 3(x-3)  <<Substitute in values

y-7 = 3x - 9   << Expand out

y = 3x - 9 + 7 << Simplify and collect like terms

y = 3x -2  << Equation in the form y = mx + c (m = 3, c = -2)

3x - y - 2 = 0  << Equation in the form ax + by + c   (a=3,  b= -1,  c = -2)

Given the Gradient and a Point

If a given the gradient, and a point its much easier. We just repeat the process using the formula, infact it's the same thing above, but easier, as we don't have to find the gradient. So just plug in the gradient and the coordinates in the formula : y - y1 = m(x- x1)

Perpendicular Lines and Parellel Lines 

* When two lines are parellel, the gradient of the lines is the same. (m)
* When two lines are perpendicular (at right angles), the product of the two gradients is equal to -1 .

Example

a) y = 4x - 3, find the equation of a line which is parellel :
Answer = Any line which has the gradient 4... y=4x + ... the y intercept does not matter.
b) Find the gradient of the line perpendicular :
Answer = Remember the product of the gradients has to be equal to -1.
So Let m be the gradient of the perpendicular line :
m x 4 = -1
m = -1/4

Transformations of Graphs

•  Edexcel - C1, Algebra and Functions
• AQA - C1,Algebra and Functions
• OCR - C1, Coordinate Geometry and Graphs

In this final post of the first chapter, we will discuss how to transform graphs. Four Transformations can be applied to graphs, and we need to be able to draw the resulting graphs from these transformations.

Transformation 1 - y = af(x)
What you do - Multiply each y coordinate of the graph by a.
How this looks graphically - It either squahes the graph vertically, or stretches it out, depending on a.
** This transformation only affects the y coordinates, the x coordinates stay the same.**

Transformation 2 - y=f(x) + a
What you do - Add a to each of the y coordinate.
How this looks graphically - It shifts the graph upwards by a units.
** Again, this transformation only affects the y-coordinates, and if it is y=f(x) - a, then simply the graph shifts downwards**

Transformation 3 - y=f(ax)
What you do - Divide each x-coordinate by a.
How this looks graphically - It Scales the graph by a factor of 1/a, parellel to the x-axis.
** This transformation only affects the x-coordinates**

Transformation 4 - y=f(x + a)
What you do - Subtract a from each x-coordinate.
How this looks graphically - It shifts the graph to the left by a units.
**This transformation only affects the x-coordinates, if it is y =f(x - a), then the graph will shift to the right by a units.**

I have attached one example with my image notes ! Will post another one tomorrow.

Notes on Transformations of Functions

Example 1

Graphs of Functions and Interpreting Graphs

•  Edexcel - C1, Algebra and Functions
• AQA - C1, Algebra
• OCR - C1,Coordinate Geometry and Graphs

Almost finished with Algebra and Functions, We now need to know how to sketch certain functions, aswell as know how to interpret graphs to solve equations, and know how to apply different transformations (this will be covered in the next post).

In the specification, it says sketching curves defined by simple equations. I shall teach you how to draw linear, quadratic and cubic functions. Though the first two you should have known from gcse. Aswell as teaching you k/x functions where k is a integer (this is a reciprocal function).

Linear Functions


So if you see a function like y=3x + 2, or y= x or y = -4x.... these are known as linear functions, simply because they are straight lines.. and are of the power 1 (exponent). We usually see them in the form y=mx + c, but we will see in the next section Coordinate Geometry, they can be rearranged in the form ax + by + c aswell. Let's focus in the form y= mx + c.

m = gradient of the function (slope)
c = y intercept

If you take y to be 0 : you will get 0 = mx + c, rearrange for x this should be the point on the function when y=0, or where it crosses the x-axis. Likewise if you make x=0, you will get y=c, this is the point on function when x =0, or where it crosses the y-axis.

To plot a function, if you take different values of x and y, you could plot it up... though we are meant to sketch functions in a general way. So Linear Functions are straight lines .. so let's take 3 examples.

a) y= 2x - 5
Firstly we know m = 2 (gradient), and c = -5 (y intercept), this is easy to see in this form, but not all linaer functions are in this form REMEMBER, y= 4x , is still a linear function even though c = 0.

y intecerpt = take x =0, so y= 2(0) - 5
y= -5

We've got a coordinate on the function which is  (0, -5)

x intercept = take y =0, so 0 = 2x - 5 so 5=2x so x = 5/2

Another coordinate is  (5/2 , 0)
As we know it is a straight line just draw a corresponding straight line using the two points :

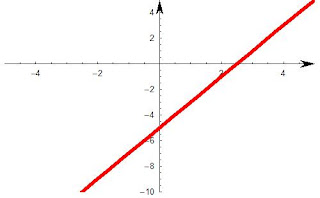Graph of y=2x-5, notice where it croses the axis, it's just a straight line through the points

b) Let's take y = -6x

Here m = -6 (negative gradient ), and c = 0

y - intercept, y = -6(0), y = 0, so when x =0, y= 0.
First coordinate (0,0)

x- intercept, y =0 so 0 = -6x so 0/-6 = x, so x =0
Second Coordinate (0,0)
As we already knew (0,0) from the first coordinate, the 2nd step was futile.. so we
 simply substitute other values to get a general shape of the graph.

when x = 1, y= -6
when x = -5, y = 30

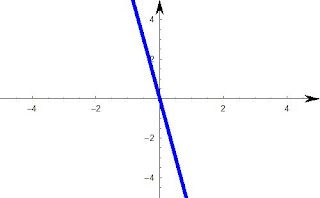Graph of y = -6x, notice the gradient (m) is negative, so it is downward sloping, and it goes through the origin (0,0).

Quadratic Graphs


As we know from the previous section, that quadratic functions are in the form ax^2 + bx + c = 0. If we have two solutions to the equation (two roots), these are the corresponding x - values where y =0, or the two x intercepts.
We know that a quadratic is a parabola shape, and the coefficient of x squared, determines whether it is a U or a upside down U. If the coefficient is negative, it is an upside down U, if positive it is a U shape. Again we know c is the y intercept ( or where x =0).  There will also be a minimum  or maximum point on the graph, (depending the parabolic nature), this can be found through differentiation (later on...).


e.g. 1 ) y = 2x^2 - 8x + 6

Firstly a =2, so it will be a U shaped parabola shape.
substitute x =0, so y= 6, the y intercept is 6. One coordinate is (0,6)

Now find the roots of the quadratic, (through one of the three methods).
 Let's do it by factorisation, divide everything by 2.

x^2 - 4x + 3 = 0

(x-3)(x-1) = 0
so x=1,3 (these are the points which the function cross the x-axis.

(1,0) and (3,0)

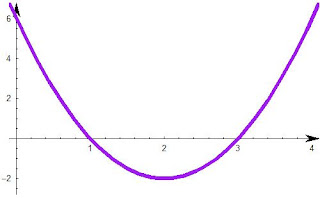Graph of example above. a) positive a, so U shape parabola, and two roots.

2nd example :
y = -x² - 4x - 3                                                             

a is -1, so it is an upside down U shape.
y intercept is -3 , (0,-3)

now solve for x :
-x² - 4x -3 = 0
-(x -1) (x-3) =0
so x =-1 and x = -3

so (-1,0) and (-3,0)

Graph of -x² - 4x -3, notice where it crosses the axis and the shape.

Cubic Functions

A cubic is in the form ax^3 + bx^2 + cx + d = 0, here again the a decides the shape... we know the cubic shape is a kind of S shape (looking at it with your head tilted). if a is negative then the graph will go from right to left, if positive, then left to right. Here's what i mean :

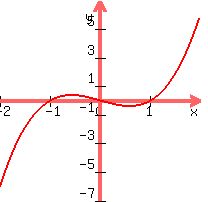When a is positive

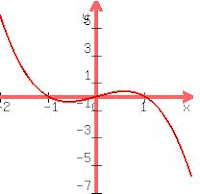When a is negative

                                
 Again we have to find the x intercepts, by setting the equation equal to 0. And solving, this can be done sometimes if you know one factor, leaving you with a quadratic, which would give you the other two. The y-intercept is found by making x=0.

A cubic will have either 3 roots, 2 roots or 1 root. (it crosses the x-axis 3 times, 2 times or once.)

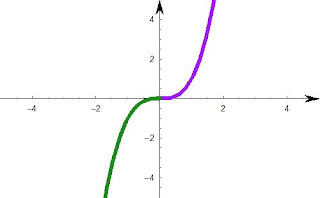Graph of x^3, notice here there is one root, at the origin (0,0).

 Example 1
y = x(x-2)(x+3)
This is a cubic, but factorised, it we were to expand it, it would give us in the form of ax^3 + bx^2 + cx + d, but when factorised it is easy to draw a cubic. We are only expected to sketch easy cubics at this stage, as solving it, is in C2 (using factor theorem, and algebraic division). If it is already factorised, it is easy to draw... for this example. We have three roots, x=0 , x =2 and x =-3, these are the points where the function cross the x-axis.Remember, so cubics can have two roots, so one may be a repeated root.

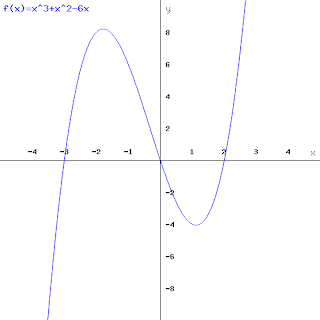Graph of the cubic (x^3 + x^2 - 6x), when expanded, notice the roots at -3,0 and 2. It has two turning points.

Example 2
x^3 -9x.
Let's try factorising this, if we take x out we get x(x^2 -9). So one root is 0, now we have x^-9. Remember a difference of two square where you have something in the form of x^2 - a. Where a is a square number, if this is the case, the roots of the equation are +root of a and -root of a. In this case a = 9, so the roots are 3 and -3.
All the roots of this cubic are -3, 0 , 3. So we have the coordinates (-3,0)  (0,0) and (3,0). The y intercept is 0.

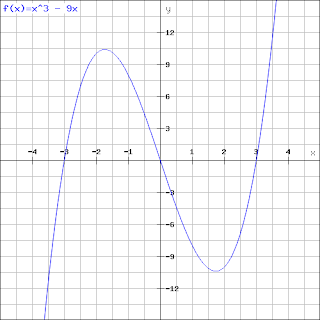Three roots at 0, -3 and 3.

Reciprocal Graphs
The reciprocal function is y = 1/x. The curve of this function looks like a hyperbola, this is the graph of 1/x :

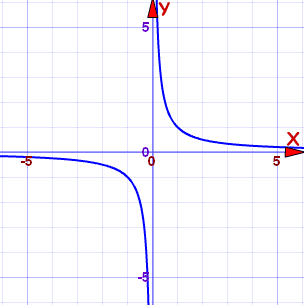Graph of 1/x

There is one special feature of graphs of the form k/x, where k is some number(and x is not 0). These graphs have a feature called Assymptotes. This graph has two assymptotes, at x=0 and y=0, meaning the graph tends to x=0, and y=0, but never never touches it, thus the shape of the graph. The x-axis is a horizontal assymptote, while the y-axis is a vertical assymptote.

Assymptote - A line where a curve gets closer and closer to but does not meet.
By substituting 0 as x or y, we can find the intercepts of the axes.
If two graphs meet, this algberically, means setting two of the equations equal to each other, the coordinates of intersection, can be found by solving.
A cubic can have one, two or three roots.

C1 - Algebra and Functions - Polynomials

Sorry to update after almost a week, was really busy with other work. In this post, I shall talk about Polynomials. A polynomial is basically, a sequence of monomials, which is a term of product of powers of variables. Confused much ?

In simple terms, we just need to know about two polynomials, one we've already encountered, is a Quadratic, this is a polynomial of degree 2. The other we learn about in this post is a Cubic, which is a polynomial of degree 3.

We are expected to factorise cubics, aswell sketch them, and manipulate them algebraically, i.e. Factorise, Collect like terms and expand brackets. A cubic takes the form :

where a is not 0, and b,c,d are constants.

Cubics, can be factorised into 3 brackets, as Quadratics can be factorised using two. Where a cubic function crosses the x-axis is known as the roots. In terms of an equation, (the solutions), when the cubic is set equal to 0.

An sketch of some cubic function looks like :

A cubic function, this one crosse the x-axis 3 times, meaning it has 3 roots/ 3 solutions.Try looking a the graph with your head tilted, and notice the kind of S shape, it is a feature of a cubic. Not all cubic functions will look like the S shape though !

Multiplying out Polynomials (Expanding Brackets)

If we have two polynomials (one a quadratic, the other linear) e.g.

(3x^2 + 2x + 8)  (x + 5), if we had to expand them, its basically saying multiply each term in one bracket with the other term in the other bracket :

Multiply 3x^2 by the second bracket we get :

3x^3 + 15x^2

Multiply 2x by the second bracket we get :

2x^2 + 10x

Multiply 8 by the second bracket we get:

8x + 40

Collect like terms and simplify :

3x^3 + 15x^2 + 2x^2 + 10x + 8x + 40

= 3x^3 + 17x^2 + 18x + 40

Notice, its in the form of a cubic, where a = 3, b = 17, c = 18 and d = 40.
Though I don't think we need to be able to solve cubics, we can if the original quadratic we had can be factorised. If it can be factorised, we would have three roots, in this case the solutions we be :

x = -5, and x = one of the solutions of quadratic, x = other solution of quadratic

C1- Algebra and Functions - Solving Quadratic and Linear Inequalities

Now we move on to Solving Inequalities. An Inequality is basically a statement comparing to variables, usually about their size. e.g. a < b (a is less than b - the value of a is less than b)

let  x = john's weight and y = rahul's weight
x < y (john's weight is less than rahul's weight)

Let's recap the different signs used in inequalities :

> is more than
< is less than
These are known as STRICT Inequalities. e.g. 7 < 13 is a strict inequality ( 7 is strictly less than 13) [This is not in the spec. - but it may be useful later on]
≥ is more than or equal to
≤ is less than or equal to. 

Rules of Inequalities

1) We are allowed to add or subtract the same number on both sides.
2) We are allowed to switch sides, and change the sign.


e.g.   4 < 5-x is the same as 5-x > 4.


3) We are allowed to multiply by the same number on both sides, But if this number is positive, the sign remains the same, if it is negative the sign has to be reversed.


e.g   [6 > 3x + 4 ] * 3 =   [18 > 9x + 12]
        [6 > 3x - 4 ] *-2 =   [-12<-6x + 8]


We we looked at so far, are examples of LINEAR Inequalities.

Solving Linear Inequalities Notes

Quadratic Inequalities 

1) Simplify this Quadratic Inequality, to get one quadratic expression. Rearrange the inequality to get it equal to 0. ( > 0, < 0 or less than equal to or more than equal to).
2) Find the roots of the equation (Solve the quadratic). The roots are called CRITICAL VALUES.
3) Draw the graph of the equation, seeing which x values satisfy the inequality,using the Critical Values.

Solving Quadratic Inequalities Notes

C1-Algebra and Functions - Solving Simultaneous Equations

We now,move on to Solving Simultaneous Equations. We will usually encounter questions where 1 equation is a quadratic and the other being a linear. From Gcse, you should know how to solve simultaneous equations by either Substituition or Elimination. Let's Recap :

1) y = 4x + 2
2) 3x + 6y =39

Let's Solve this firstly by Substituition:

* In General, we rearrange one of the equations to make x or y the subject, we then substitute this expression in the 2nd equation, to find one of the variables.

*Simply then plug into any equation, to find the value of the other variable.

We see y is already the subject of the first equation, let's substitute this equation as y in the 2nd equation so :
3x + 6(4x+2) = 39
Now expand and simplify:
3x + 24x + 12 = 39
27x =27
x= 1
Now Substitute this value of x=1, into any equation to find the value for y:
y=4(1) + 2
y=6

Solutions {x=1,y=6}

By Elimination
*In General, We usually eliminate one of the variables x or y, we do this by making the coefficient of the x's or y's same and the subtracting or adding them to make it 0.
*Now we only have one variable, so we solve for this variable. And substitute the value in one of the equations to get the value for the other variable.

1) y = 4x + 2
2) 3x + 6y =39

We can use either make the coefficient of x or y the same, we'll stick for y, it's easier in this case. Multiply the first equation by 6 :
6y = 24x + 12

Now rearrange the second equation to make 6y the subject :
6y = 39 - 3x

Subtract these two new equations :
       6y = 12 + 24x

   -   6y = 39 - 3x 
 which gives you :
0 = -27 + 27x
rearrange to solve for x:
27= 27x
x= 27/27 = 1


Now substitute this value in any of our two original equations for y :
y= 4(1)+2
y=6


Solutions = {1,6}


That shows how to solve two linear equations / simultaneous equations. To Solve a Simultaneous equation system with a quadratic, simply use Substituition :

1) Rearrange the the linear equation to make x or y the subject.
2) Substitute this expression for x/y, in the quadratic equation. Solve for this variable
3)Substitute the value you get, into either of the two original equations {linear or quadratic} to find the other variable's value.

I don't want to make this post too long, so i will add an example in my set of image notes.

Notes for Just "Simultaneous Equations"

Here is an example with Simultaneous with a quadratic involved:

Simultaneous With a Quadratic Equation

*Note - The example I have used kind of uses everything we learnt from the previous topics - Using how to solve a quadratic to manipulating surds. The answers are left in "Exact Values", i.e. not in decimals. Be sure that edexcel can test you in anyway way.